2304. Horrible Queries
World is getting more evil and it’s getting tougher to get
into the Evil League of Evil. Since the legendary Bad Horse has retired, now
you have to correctly answer the evil questions of Dr. Horrible, who has a PhD
in horribleness (but not in Computer Science). You are given an array of n elements, which are initially all 0.
After that you will be given c
commands. They are:
·
0 p q
v – you have to add v to all
numbers in the range of p to q inclusive, where p and q are two indexes
of the array.
·
1 p q – print a line containing a single
integer which is the sum of all the array elements between p and q inclusive.
Input. The
first line contains the number of test cases. Each test case starts with n (n ≤ 105) and c (c
≤ 105).
After that you'll be given c commands
in the format as mentioned above. It is known that 1 ≤ p, q
≤ n and 1 ≤ v ≤ 107.
Output. Print the answers to the queries.
|
Sample
input |
Sample
output |
|
1 8 6 0 2 4 26 0 4 8 80 0 4 5 20 1 8 8 0 5 7 14 1 4 8 |
80 508 |
SOLUTION
data structures – segment tree
Algorithm analysis
Для решения
задачи следует реализовать дерево отрезков, поддерживающее групповую
модификацию – прибавление и суммирование.
В каждом узле
дерева будут поддерживаться значения двух переменных: суммы на отрезке summa и некоторого дополнительного
значения add, которое следует
прибавить ко всем элементам отрезка. Протолкнуть
значение add по дереву на один
уровень ниже означает прибавить его к значению summa левого и правого поддерева, умноженного на длину
соответствующего отрезка, а также к значению add левого и правого поддерева, тем самым рекурсивно обеспечив
проталкивание значения add до листьев
дерева.

Операцию
проталкивания следует производить не только при выполнении операции прибавления
на отрезке, но и при вычислении сумм.
Example
Пусть некоторая
вершина соответствует отрезку [0; 5]. Ее сыновьями являются отрезки [0; 2] и
[3; 5]. Рассмотрим операцию проталкивания на примере.
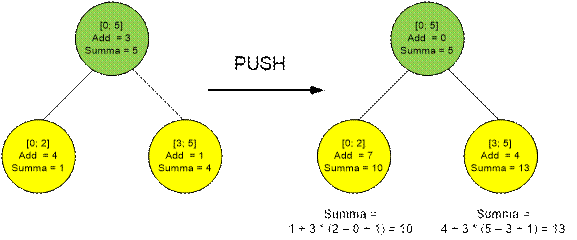
Algorithm
realization
Дерево отрезков храним в виде массива t структур node длины MAX, где MAX – максимальное количество элементов, которое
может храниться в отрезке.
#define MAX 100000
struct node
{
long long summa, add;
} SegTree[4*MAX];
Функция Push производит
проталкивание значения add вершины v в сыновья. Если add ≠ 0, то его следует
протолкнуть на один уровень вниз. После проталкивания значение add в
вершине v ставим равным 0.
void Push(int v, int lpos, int mid, int rpos)
{
if (SegTree[v].add == 0) return;
SegTree[2*v].add += SegTree[v].add;
SegTree[2*v].summa += (mid - lpos + 1) * SegTree[v].add;
SegTree[2*v+1].add += SegTree[v].add;
SegTree[2*v+1].summa += (rpos - mid) * SegTree[v].add;
SegTree[v].add = 0;
}
Функция AddValue прибавляет ко всем элементам отрезка [left; right] значение val. Вершине v соответствует отрезок [lpos; rpos].
void AddValue(int v, int lpos, int rpos, int left, int right, int val)
{
if (left > right) return;
Если [left; right] соответствует отрезку, который
хранится в вершине дерева [lpos; rpos], то прибавляем в текущей вершине дерева переменным add и summa соответствующие значения.
if ((lpos == left) && (rpos == right))
{
SegTree[v].add += val;
SegTree[v].summa += 1LL * (right - left + 1) * val;
return;
}
Находим середину отрезка mid = (lpos + rpos)
/ 2.
int mid = (lpos + rpos) / 2;
Проведем проталкивание, если add не равно нулю.
Push(v, lpos, mid, rpos);
Рекурсивно обрабатываем левого и
правого сына текущей вершины дерева отрезков.
AddValue(2*v, lpos, mid, left, min(mid, right), val);
AddValue(2*v+1, mid+1, rpos, max(left, mid + 1), right, val);
Пересчитываем значение суммы в
вершине v через значения сумм ее
детей.
SegTree[v].summa = SegTree[2*v].summa + SegTree[2*v+1].summa;
}
Функция Summa возвращает значение суммы на
отрезке [left; right]. Вершине v соответствует отрезок
[lpos; rpos].
long long Summa(int v, int lpos, int rpos, int left, int right)
{
if (left > right) return 0;
Если [left; right] совпадает с отрезком [lpos; rpos], который хранится в вершине v дерева, то возвращаем находящееся в ней значение суммы.
if ((lpos == left) && (rpos == right))
return SegTree[v].summa;
Находим середину отрезка mid = (lpos + rpos)
/ 2.
int mid =
(lpos + rpos) / 2;
Проведем проталкивание, если add не равно нулю.
Push(v, lpos, mid, rpos);
Разбиваем отрезок [lpos; rpos] на [lpos; mid] и [mid + 1; right]. Запускаем рекурсивно вычисление сумм на подотрезках.
Складываем полученные суммы.
return Summa(2*v, lpos, mid, left, min(mid, right)) +
Summa(2*v+1, mid+1, rpos, max(left, mid+1), right);
}
Основная часть
программы.
scanf("%d",&tests);
while(tests--)
{
Для каждого теста читаем входные данные и строим дерево
отрезков. Поскольку изначально все элементы дерева отрезков равны нулю
(значение add каждой вершины можно
проинициализировать нулем, так как по условию задачи в командах прибавляемое
значение всегда натурально и не может равняться нулю), то в качестве
инициализации достаточно просто заполнить нулями массив SegTree. Функцию
построения дерева отрезков можно не использовать.
scanf("%d
%d",&n,&c);
memset(SegTree,0,sizeof(SegTree));
Последовательно обрабатываем c команд.
for(i = 0; i
< c; i++)
{
scanf("%d
%d %d",&command,&p,&q);
if (command
== 0)
{
scanf("%d",&v);
AddValue(1,1,n,p,q,v);
} else
printf("%lld\n",Summa(1,1,n,p,q));
}
}
Реализация с помощью класса
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
class SegmentTree
{
public:
const static int NONE_ASSIGN = 0;
vector<long long> Summa, Add;
int len;
SegmentTree(int n)
{
len = n;
Summa.resize(4*n);
Add.resize(4*n);
BuildZeroTree(1, 1, len);
}
void BuildZeroTree(int v, int lpos, int rpos)
{
if (lpos == rpos)
{
Summa[v] = 0;
Add[v] = NONE_ASSIGN;
}
else
{
int mid = (lpos + rpos) / 2;
BuildZeroTree(2*v, lpos, mid);
BuildZeroTree(2*v+1, mid + 1, rpos);
Summa[v] = Summa[2*v] + Summa[2*v+1];
Add[v] = NONE_ASSIGN;
}
}
void Push(int v, int lpos, int mid, int rpos)
{
if (Add[v] == NONE_ASSIGN) return;
Add[2*v] += Add[v];
Summa[2*v] += (mid - lpos + 1) * Add[v];
Add[2*v+1] += Add[v];
Summa[2*v+1] += (rpos - mid) * Add[v];
Add[v] = NONE_ASSIGN;
}
void AddValue(int left, int right, int val)
{
AddValue(1, 1, len, left, right, val);
}
void AddValue(int v, int lpos, int rpos,
int left, int right, int val)
{
if (left > right) return;
if ((lpos == left) && (rpos == right))
{
Add[v] += val;
Summa[v] += (long long)(right - left + 1) * val;
return;
}
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
AddValue(2*v, lpos, mid, left, min(mid, right), val);
AddValue(2*v+1, mid+1, rpos, max(left, mid+1), right, val);
Summa[v] = Summa[2*v] + Summa[2*v+1];
}
long long Sum(int left, int right)
{
return Sum(1, 1, len, left, right);
}
long long Sum(int v, int lpos, int rpos, int left, int right)
{
if (left > right) return 0;
if ((lpos == left) && (rpos == right)) return Summa[v];
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
return Sum(2*v, lpos, mid, left, min(mid, right)) +
Sum(2*v+1, mid+1, rpos, max(left, mid+1), right);
}
};
int i, n, c, tests, command;
int L, R, p, q, v;
int main(void)
{
scanf("%d", &tests);
while (tests--)
{
scanf("%d %d", &n, &c);
SegmentTree s(n);
for (i = 0; i < c; i++)
{
scanf("%d %d %d", &command, &p, &q);
if (command == 0)
{
scanf("%d", &v);
s.AddValue(p, q, v);
}
else printf("%lld\n", s.Sum(p, q));
}
}
return 0;
}